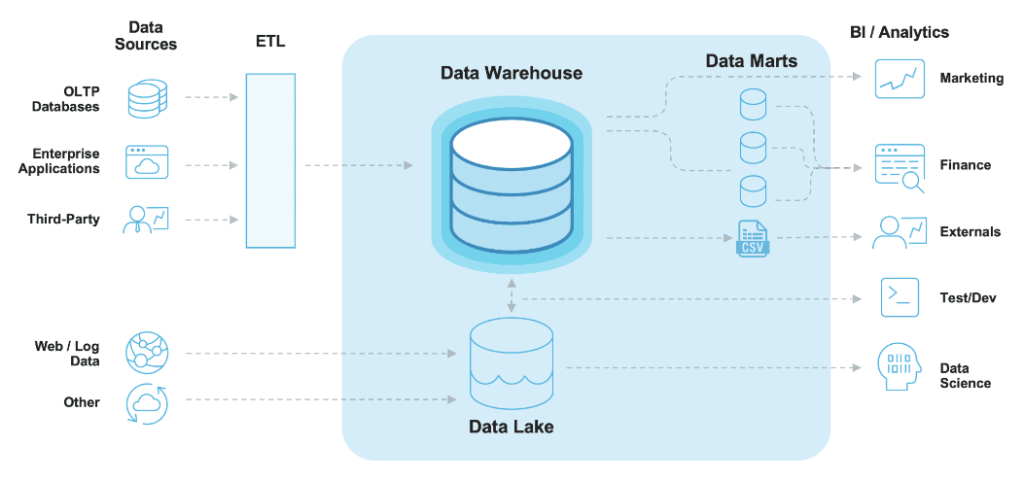
Requirement

A system is required to automatically categorise any source (eg person) into a “type” from a questionnaire or other results – which can then be used for identification, focus, marketing etc.

Case Study

Here, a set of 19 questions (each agreement rated from 0 to 100) from 48,645 people about their attitudes towards music is taken from www.kaggle.com/c/MusicHackathon. Our aim is to group the questions to identify clusters containing similar answers, so that users can be classified.

Executive Summary

We use Exploratory Factor Analysis to identify and summarise the exact questions within each group including our interpreted description of those 8 groups (from 19 Questions). This is backed up by checking against a Correlation Matrix and Network of the variable connections, which verify the groupings:

Group 1: ‘Cutting Edge’
Group 2: ‘Music Searchers’
Group 3: ‘Fun to Escape’
Group 4: ‘Technology Buffs’
Group 5: ‘Partiers’
Group 6: ‘Out of Touch’
Group 7: ‘Non Payers’
Group 8: ‘Proud Owners’

We could have more or (more likely) less groupings, but this seems a good level for marketing, reach-out and other focus. They can be combined if necessary, but good to maintain this granularity.

Data Preparation

Records are fairly clean, but best to remove users who’s responses failed to answer all questions (lazy or time-pressed answering may indicate sloppiness on answered questions) as we have enough full responses in sample.

Responses are checked for normality of distribution across all scores – they all show a similar pattern and the first 4 questions are shown as histograms. ## RESPID GENDER AGE WORKING REGION ## 36927 36927 Female 60 Other South ## 3566 3566 Female 36 Full-time housewife / househusband South ## 20054 20054 Female 52 Employed 30+ hours a week Midlands ## 41749 41749 Female 40 Employed 8-29 hours per week South ## 23108 23108 Female 16 Full-time student North ## 42754 42754 Male 20 Temporarily unemployed Midlands ## MUSIC LIST_OWN ## 36927 Music is important to me but not necessarily more important 1 hour ## 3566 Music is important to me but not necessarily more important 1 hour ## 20054 I like music but it does not feature heavily in my life 1 hour ## 41749 Music means a lot to me and is a passion of mine 2 hours ## 23108 Music means a lot to me and is a passion of mine 3 hours ## 42754 Music means a lot to me and is a passion of mine 5 hours ## LIST_BACK Q01 Q02 Q03 Q04 Q05 Q06 Q07 Q08 Q09 Q10 Q11 Q12 ## 36927 49 50 49 50 32 33 32 0 74 50 50 71 ## 3566 1 hour 55 55 62 9 9 9 10 11 55 12 65 65 ## 20054 Less than an hour 11 50 9 8 45 10 30 29 8 50 94 51 ## 41749 3 hours 81 80 88 88 31 31 51 30 8 76 74 64 ## 23108 6 hours 76 79 78 73 71 68 73 67 31 56 13 82 ## 42754 74 100 100 54 54 18 53 27 5 100 72 73 ## Q13 Q14 Q15 Q16 Q17 Q18 Q19 ## 36927 52 71 9 7 72 49 26 ## 3566 80 79 51 31 68 54 33 ## 20054 74 66 27 46 73 8 31 ## 41749 73 85 61 77 76 78 88 ## 23108 79 68 71 NA 86 80 32 ## 42754 100 100 75 74 76 34 73

The data distributions are not completely normal (the means are not centred around the central 50) and show around 5 potential peaks around the score ranges 10, 30, 50, 70 and less pronounced after 90. This indicates an option bias where likely it was easier to select such values. However, if we restrict the frequencies to only 5 bins, we can see more normal distributions:

These distributions are still spread across all ranges rather than centralised, but not compeletly skewed, so acceptable for our purpose of correlation and factor analysis.

Exploratory Factor Analysis

First we need to decide on number of groupings (factors) to split by, so use a Scree Plot to see how many levels are distributed.

## Parallel analysis suggests that the number of factors = 8 and the number of components = 4

8 levels looks like they describe most of the variation, and is recommended. More than that will be too many arbitrary groups, and less would lose some grouping which may be beneficial to identify. We can only be sure once the groupings have been inspected for meaning.

Orthoganal (non rotated) Factor Analysis

Let’s have a look at orthoganal (non rotated) Factor Analysis of the 8 groups. ## Factor Analysis using method = wls ## Call: fa(r = quest.set, nfactors = 8, rotate = “none”, fm = “wls”) ## Standardized loadings (pattern matrix) based upon correlation matrix ## WLS1 WLS2 WLS3 WLS4 WLS5 WLS6 WLS7 WLS8 h2 u2 com ## Q01 0.78 -0.24 0.16 0.05 0.01 0.18 0.17 -0.03 0.76 0.24 1.5 ## Q02 0.64 -0.24 -0.03 -0.11 0.04 0.15 0.20 -0.04 0.55 0.45 1.7 ## Q03 0.82 -0.24 0.10 0.05 0.03 0.14 0.22 -0.02 0.80 0.20 1.4 ## Q04 0.40 0.42 0.18 0.45 -0.01 -0.03 0.05 -0.09 0.58 0.42 3.5 ## Q05 0.25 0.54 0.27 0.46 -0.01 0.01 -0.01 0.02 0.63 0.37 2.9 ## Q06 -0.04 0.46 0.28 -0.27 0.60 0.20 -0.04 0.01 0.77 0.23 3.1 ## Q07 0.42 0.58 0.07 -0.34 -0.27 -0.03 0.10 -0.02 0.71 0.29 3.1 ## Q08 0.44 0.55 0.14 -0.34 -0.26 -0.05 0.06 0.02 0.71 0.29 3.4 ## Q09 -0.33 0.28 0.11 0.16 0.06 0.02 0.07 0.11 0.25 0.75 3.2 ## Q10 0.59 -0.18 0.01 0.09 0.00 0.03 0.07 0.19 0.43 0.57 1.5 ## Q11 0.45 0.32 -0.74 0.04 0.07 0.13 -0.02 0.02 0.88 0.12 2.2 ## Q12 0.50 0.29 -0.58 0.07 0.06 0.07 -0.02 0.05 0.69 0.31 2.6 ## Q13 0.74 0.01 -0.05 -0.04 0.24 -0.46 0.03 -0.04 0.83 0.17 2.0 ## Q14 0.74 -0.09 -0.04 -0.03 0.18 -0.31 0.07 -0.02 0.69 0.31 1.5 ## Q15 0.79 -0.12 0.16 -0.04 -0.01 0.01 -0.15 0.32 0.79 0.21 1.6 ## Q16 0.72 0.00 0.07 0.05 -0.11 -0.07 -0.12 0.06 0.55 0.45 1.2 ## Q17 0.64 -0.01 -0.11 0.10 -0.03 0.07 -0.01 -0.11 0.45 0.55 1.2 ## Q18 0.87 -0.08 0.10 -0.06 -0.04 0.09 -0.28 -0.19 0.90 0.10 1.4 ## Q19 0.83 -0.10 0.15 -0.03 -0.01 0.09 -0.18 -0.04 0.77 0.23 1.2 ## ## WLS1 WLS2 WLS3 WLS4 WLS5 WLS6 WLS7 WLS8 ## SS loadings 7.28 1.82 1.22 0.79 0.62 0.48 0.30 0.22 ## Proportion Var 0.38 0.10 0.06 0.04 0.03 0.03 0.02 0.01 ## Cumulative Var 0.38 0.48 0.54 0.58 0.62 0.64 0.66 0.67 ## Proportion Explained 0.57 0.14 0.10 0.06 0.05 0.04 0.02 0.02 ## Cumulative Proportion 0.57 0.71 0.81 0.87 0.92 0.96 0.98 1.00 ## ## Mean item complexity = 2.1 ## Test of the hypothesis that 8 factors are sufficient. ## ## The degrees of freedom for the null model are 171 and the objective function was 10.69 with Chi Square of 310812 ## The degrees of freedom for the model are 47 and the objective function was 0.07 ## ## The root mean square of the residuals (RMSR) is 0.01 ## The df corrected root mean square of the residuals is 0.02 ## ## The harmonic number of observations is 29085 with the empirical chi square 638 with prob < 1.2e-104 ## The total number of observations was 29085 with Likelihood Chi Square = 1962 with prob < 0 ## ## Tucker Lewis Index of factoring reliability = 0.978 ## RMSEA index = 0.037 and the 90 % confidence intervals are 0.036 0.039 ## BIC = 1479 ## Fit based upon off diagonal values = 1 ## Measures of factor score adequacy ## WLS1 WLS2 WLS3 WLS4 WLS5 ## Correlation of (regression) scores with factors 0.98 0.93 0.93 0.83 0.85 ## Multiple R square of scores with factors 0.97 0.86 0.87 0.69 0.72 ## Minimum correlation of possible factor scores 0.94 0.72 0.73 0.39 0.43 ## WLS6 WLS7 WLS8 ## Correlation of (regression) scores with factors 0.84 0.77 0.70 ## Multiple R square of scores with factors 0.70 0.60 0.49 ## Minimum correlation of possible factor scores 0.40 0.20 -0.02

Then compare that to the same FA but with only 5 factors: ## Factor Analysis using method = wls ## Call: fa(r = quest.set, nfactors = 5, rotate = “none”, fm = “wls”) ## Standardized loadings (pattern matrix) based upon correlation matrix ## WLS1 WLS2 WLS3 WLS4 WLS5 h2 u2 com ## Q01 0.78 -0.25 0.15 0.05 -0.15 0.72 0.28 1.4 ## Q02 0.64 -0.25 -0.04 -0.08 -0.10 0.49 0.51 1.4 ## Q03 0.81 -0.24 0.09 0.06 -0.11 0.74 0.26 1.2 ## Q04 0.39 0.41 0.22 0.37 0.00 0.51 0.49 3.5 ## Q05 0.25 0.57 0.34 0.45 -0.02 0.71 0.29 3.0 ## Q06 -0.03 0.30 0.14 -0.08 0.08 0.12 0.88 1.8 ## Q07 0.41 0.57 0.09 -0.39 -0.05 0.66 0.34 2.8 ## Q08 0.45 0.56 0.17 -0.45 -0.04 0.75 0.25 3.1 ## Q09 -0.33 0.28 0.12 0.15 0.02 0.22 0.78 2.7 ## Q10 0.58 -0.18 0.01 0.09 -0.04 0.38 0.62 1.3 ## Q11 0.46 0.34 -0.73 0.09 -0.10 0.87 0.13 2.3 ## Q12 0.50 0.31 -0.57 0.10 -0.05 0.69 0.31 2.6 ## Q13 0.75 -0.01 -0.06 -0.01 0.56 0.87 0.13 1.9 ## Q14 0.74 -0.10 -0.05 0.00 0.33 0.67 0.33 1.4 ## Q15 0.77 -0.12 0.13 -0.03 -0.03 0.63 0.37 1.1 ## Q16 0.71 0.00 0.08 0.01 -0.01 0.52 0.48 1.0 ## Q17 0.64 -0.01 -0.10 0.09 -0.09 0.44 0.56 1.1 ## Q18 0.85 -0.09 0.09 -0.05 -0.08 0.75 0.25 1.1 ## Q19 0.83 -0.11 0.14 -0.03 -0.09 0.73 0.27 1.1 ## ## WLS1 WLS2 WLS3 WLS4 WLS5 ## SS loadings 7.23 1.76 1.19 0.78 0.51 ## Proportion Var 0.38 0.09 0.06 0.04 0.03 ## Cumulative Var 0.38 0.47 0.54 0.58 0.60 ## Proportion Explained 0.63 0.15 0.10 0.07 0.04 ## Cumulative Proportion 0.63 0.78 0.89 0.96 1.00 ## ## Mean item complexity = 1.9 ## Test of the hypothesis that 5 factors are sufficient. ## ## The degrees of freedom for the null model are 171 and the objective function was 10.69 with Chi Square of 310812 ## The degrees of freedom for the model are 86 and the objective function was 0.44 ## ## The root mean square of the residuals (RMSR) is 0.02 ## The df corrected root mean square of the residuals is 0.03 ## ## The harmonic number of observations is 29085 with the empirical chi square 4564 with prob < 0 ## The total number of observations was 29085 with Likelihood Chi Square = 12911 with prob < 0 ## ## Tucker Lewis Index of factoring reliability = 0.918 ## RMSEA index = 0.072 and the 90 % confidence intervals are 0.071 0.073 ## BIC = 12027 ## Fit based upon off diagonal values = 1 ## Measures of factor score adequacy ## WLS1 WLS2 WLS3 WLS4 WLS5 ## Correlation of (regression) scores with factors 0.98 0.92 0.92 0.84 0.86 ## Multiple R square of scores with factors 0.96 0.85 0.85 0.71 0.75 ## Minimum correlation of possible factor scores 0.92 0.69 0.71 0.41 0.50

Then only 4 factors (only summary output this time): ## ## Factor analysis with Call: fa(r = quest.set, nfactors = 4, rotate = “none”, fm = “wls”) ## ## Test of the hypothesis that 4 factors are sufficient. ## The degrees of freedom for the model is 101 and the objective function was 0.76 ## The number of observations was 29085 with Chi Square = 22219 with prob < 0 ## ## The root mean square of the residuals (RMSA) is 0.03 ## The df corrected root mean square of the residuals is 0.04 ## ## Tucker Lewis Index of factoring reliability = 0.879 ## RMSEA index = 0.087 and the 10 % confidence intervals are 0.086 0.088 ## BIC = 21181NULL

Whichever number of factors we choose, the Factor Analysis will spread the loadings across that number – it will give us a Root Mean Squared Error Approximation RMSEA and Bayesian Information Criterion BIC for comparison on the same number of factors, but this doesn’t help when needing to decide on the number of factors. It’s best to check the weightings of the PA components to see if they make sense. Before deciding, it’s best to try oblique rotated factors, which will allow weightings to be shared and improve groupings.

Rotated / Oblique Factor Analysis

Now we’ll try similar but with rotated, or oblique FA – first with 8 factors again. ## Factor Analysis using method = pa ## Call: fa(r = quest.set, nfactors = 8, rotate = “oblimin”, max.iter = 100, ## fm = “pa”) ## Standardized loadings (pattern matrix) based upon correlation matrix ## PA1 PA7 PA3 PA5 PA2 PA4 PA6 PA8 h2 u2 com ## Q01 0.17 0.72 -0.04 -0.01 -0.01 0.07 0.00 0.04 0.76 0.24 1.1 ## Q02 -0.03 0.73 0.07 0.04 0.06 -0.13 0.02 -0.03 0.56 0.44 1.1 ## Q03 0.04 0.79 0.00 0.07 0.01 0.08 -0.03 0.03 0.80 0.20 1.0 ## Q04 -0.02 0.10 0.02 0.07 0.01 0.76 -0.04 -0.08 0.63 0.37 1.1 ## Q05 0.05 -0.08 0.01 -0.05 0.04 0.72 0.07 0.09 0.60 0.40 1.1 ## Q06 0.03 0.02 0.01 0.04 0.02 0.02 0.76 -0.01 0.57 0.43 1.0 ## Q07 -0.04 0.03 0.04 -0.02 0.82 0.02 0.00 -0.03 0.68 0.32 1.0 ## Q08 0.03 -0.01 -0.04 0.01 0.85 -0.01 0.01 0.02 0.74 0.26 1.0 ## Q09 -0.34 -0.08 -0.01 -0.09 0.01 0.24 0.15 0.19 0.28 0.72 3.3 ## Q10 0.06 0.33 0.09 0.09 -0.03 -0.01 -0.09 0.40 0.52 0.48 2.4 ## Q11 -0.01 0.00 0.95 -0.03 0.00 -0.01 0.01 -0.02 0.87 0.13 1.0 ## Q12 0.03 -0.02 0.79 0.05 0.01 0.04 -0.01 0.04 0.69 0.31 1.0 ## Q13 0.01 -0.06 0.01 0.92 0.01 0.01 0.02 -0.01 0.82 0.18 1.0 ## Q14 0.00 0.14 0.02 0.72 -0.01 -0.01 -0.01 0.02 0.70 0.30 1.1 ## Q15 0.54 0.09 -0.02 0.12 0.06 -0.03 -0.01 0.23 0.68 0.32 1.6 ## Q16 0.51 -0.05 0.02 0.15 0.12 0.10 -0.16 0.09 0.56 0.44 1.7 ## Q17 0.28 0.23 0.22 0.04 0.00 0.13 -0.10 -0.06 0.45 0.55 3.9 ## Q18 0.87 0.02 0.04 0.02 0.02 0.01 0.01 -0.06 0.84 0.16 1.0 ## Q19 0.82 0.07 0.01 0.00 0.00 0.02 0.04 0.03 0.79 0.21 1.0 ## ## PA1 PA7 PA3 PA5 PA2 PA4 PA6 PA8 ## SS loadings 2.78 2.38 1.70 1.78 1.52 1.29 0.70 0.38 ## Proportion Var 0.15 0.13 0.09 0.09 0.08 0.07 0.04 0.02 ## Cumulative Var 0.15 0.27 0.36 0.45 0.53 0.60 0.64 0.66 ## Proportion Explained 0.22 0.19 0.14 0.14 0.12 0.10 0.06 0.03 ## Cumulative Proportion 0.22 0.41 0.55 0.69 0.81 0.91 0.97 1.00 ## ## With factor correlations of ## PA1 PA7 PA3 PA5 PA2 PA4 PA6 PA8 ## PA1 1.00 0.81 0.33 0.70 0.41 0.28 -0.16 0.29 ## PA7 0.81 1.00 0.29 0.65 0.23 0.15 -0.24 0.29 ## PA3 0.33 0.29 1.00 0.42 0.34 0.19 -0.10 0.03 ## PA5 0.70 0.65 0.42 1.00 0.36 0.24 -0.12 0.25 ## PA2 0.41 0.23 0.34 0.36 1.00 0.38 0.23 0.10 ## PA4 0.28 0.15 0.19 0.24 0.38 1.00 0.16 0.18 ## PA6 -0.16 -0.24 -0.10 -0.12 0.23 0.16 1.00 -0.06 ## PA8 0.29 0.29 0.03 0.25 0.10 0.18 -0.06 1.00 ## ## Mean item complexity = 1.4 ## Test of the hypothesis that 8 factors are sufficient. ## ## The degrees of freedom for the null model are 171 and the objective function was 10.69 with Chi Square of 310812 ## The degrees of freedom for the model are 47 and the objective function was 0.07 ## ## The root mean square of the residuals (RMSR) is 0.01 ## The df corrected root mean square of the residuals is 0.01 ## ## The harmonic number of observations is 29085 with the empirical chi square 569.6 with prob < 7.1e-91 ## The total number of observations was 29085 with Likelihood Chi Square = 2137 with prob < 0 ## ## Tucker Lewis Index of factoring reliability = 0.976 ## RMSEA index = 0.039 and the 90 % confidence intervals are 0.038 0.041 ## BIC = 1653 ## Fit based upon off diagonal values = 1 ## Measures of factor score adequacy ## PA1 PA7 PA3 PA5 PA2 ## Correlation of (regression) scores with factors 0.96 0.95 0.95 0.94 0.92 ## Multiple R square of scores with factors 0.93 0.90 0.91 0.89 0.85 ## Minimum correlation of possible factor scores 0.85 0.80 0.81 0.77 0.69 ## PA4 PA6 PA8 ## Correlation of (regression) scores with factors 0.88 0.79 0.66 ## Multiple R square of scores with factors 0.77 0.63 0.44 ## Minimum correlation of possible factor scores 0.53 0.26 -0.12

And then with only 5 factors: ## Factor Analysis using method = pa ## Call: fa(r = quest.set, nfactors = 5, rotate = “oblimin”, fm = “pa”) ## Standardized loadings (pattern matrix) based upon correlation matrix ## PA1 PA3 PA2 PA5 PA4 h2 u2 com ## Q01 0.91 -0.05 -0.05 -0.05 0.03 0.72 0.28 1.0 ## Q02 0.68 0.08 0.01 0.00 -0.16 0.49 0.51 1.1 ## Q03 0.86 0.01 -0.06 0.01 0.02 0.74 0.26 1.0 ## Q04 0.12 0.06 -0.01 0.06 0.65 0.51 0.49 1.1 ## Q05 -0.02 0.00 0.02 -0.02 0.84 0.70 0.30 1.0 ## Q06 -0.25 -0.10 0.27 0.09 0.14 0.13 0.87 3.1 ## Q07 0.00 0.07 0.78 -0.02 0.02 0.65 0.35 1.0 ## Q08 0.03 -0.02 0.86 0.01 0.00 0.75 0.25 1.0 ## Q09 -0.38 -0.05 0.01 -0.05 0.30 0.22 0.78 2.0 ## Q10 0.57 0.06 -0.11 0.07 0.03 0.38 0.62 1.1 ## Q11 -0.03 0.94 0.02 -0.02 -0.02 0.85 0.15 1.0 ## Q12 0.03 0.79 0.01 0.05 0.04 0.70 0.30 1.0 ## Q13 -0.04 0.01 0.01 0.95 0.01 0.86 0.14 1.0 ## Q14 0.23 0.04 -0.03 0.64 -0.02 0.67 0.33 1.3 ## Q15 0.68 -0.05 0.09 0.13 0.02 0.63 0.37 1.1 ## Q16 0.54 0.04 0.10 0.13 0.10 0.52 0.48 1.3 ## Q17 0.52 0.25 -0.03 0.01 0.08 0.44 0.56 1.5 ## Q18 0.76 0.03 0.13 0.06 0.01 0.75 0.25 1.1 ## Q19 0.78 -0.03 0.11 0.04 0.04 0.73 0.27 1.1 ## ## PA1 PA3 PA2 PA5 PA4 ## SS loadings 5.20 1.71 1.56 1.66 1.32 ## Proportion Var 0.27 0.09 0.08 0.09 0.07 ## Cumulative Var 0.27 0.36 0.45 0.53 0.60 ## Proportion Explained 0.45 0.15 0.14 0.15 0.12 ## Cumulative Proportion 0.45 0.60 0.74 0.88 1.00 ## ## With factor correlations of ## PA1 PA3 PA2 PA5 PA4 ## PA1 1.00 0.34 0.32 0.70 0.20 ## PA3 0.34 1.00 0.31 0.41 0.17 ## PA2 0.32 0.31 1.00 0.34 0.38 ## PA5 0.70 0.41 0.34 1.00 0.21 ## PA4 0.20 0.17 0.38 0.21 1.00 ## ## Mean item complexity = 1.3 ## Test of the hypothesis that 5 factors are sufficient. ## ## The degrees of freedom for the null model are 171 and the objective function was 10.69 with Chi Square of 310812 ## The degrees of freedom for the model are 86 and the objective function was 0.45 ## ## The root mean square of the residuals (RMSR) is 0.02 ## The df corrected root mean square of the residuals is 0.03 ## ## The harmonic number of observations is 29085 with the empirical chi square 4563 with prob < 0 ## The total number of observations was 29085 with Likelihood Chi Square = 12939 with prob < 0 ## ## Tucker Lewis Index of factoring reliability = 0.918 ## RMSEA index = 0.072 and the 90 % confidence intervals are 0.071 0.073 ## BIC = 12055 ## Fit based upon off diagonal values = 1 ## Measures of factor score adequacy ## PA1 PA3 PA2 PA5 PA4 ## Correlation of (regression) scores with factors 0.97 0.94 0.92 0.95 0.89 ## Multiple R square of scores with factors 0.94 0.89 0.84 0.90 0.78 ## Minimum correlation of possible factor scores 0.88 0.79 0.68 0.80 0.57

Checking the weightings (by marking off the highest loading for each question in each component), it seems that the best grouping includes shared correlations which is allowed in Rotated / Oblique FA, and the 8 factor groupings are as accurately split to summarise the responses as the 4 factor ones, so we will go with the former, which assigns:

Factor 1: ‘Cutting Edge’

Q15 People often ask my advice on music – what to listen to.
Q16 I would be willing to pay for the opportunity to buy new music pre-release.
Q18 I like to be at the cutting edge of new music.
Q19 I like to know about music before other people.

Factor 2: ‘Music Searchers’

Q1 I enjoy actively searching for and discovering music that I have never heard before.
Q2 I find it easy to find new music.
Q3 I am constantly interested in and looking for more music.

Factor 3: ‘Fun to Escape’

Q11 Pop music is fun.
Q12 Pop music helps me to escape.

Factor 4: ‘Technology Buffs’

Q13 I want a multi media experience at my fingertips wherever I go.
Q14 I love technology.

Factor 5: ‘Partiers’

Q7 I enjoy music primarily from going out to dance.
Q8 Music for me is all about nightlife and going out.

Factor 6: ‘Out of Touch’

Q4 I would like to buy new music but I don’t know what to buy.
Q5 I used to know where to find music.
Q9 I am out of touch with new music.

Factor 7: ‘Non Payers’

Q6 I am not willing to pay for music.

Factor 8: ‘Proud Owners’

Q10 My music collection is a source of pride.

We can plot the resulting FA which matches our assignments:

Check Basic Correlation

Now we have more controlled groupings, check them against basic variable correlation to ensure validity.

Tracing the connections, we can see that our EFA groupings do correspond to the variable correlations – eg. Q7 and Q8 strongly correlated, so is the grouping of Q1 with Q2, Q3, Q10, Q15 and Q18 (with negative correlation to Q9).

This is confirmed further with a network graph, where we can see the strength as well as connections.

Conclusion

Several methods could be employed to group questions from their responses, for example various K-Means algorithms. However, EFA was chosen as it’s fast and in this case, effectively grouped the Questions into understandable categories.